ESTADISTICA

DOCENTE: SAMUEL RODRIGUEZ ISAZA


TEMA: MEDIDAS DE TENDENCIA CENTRAL

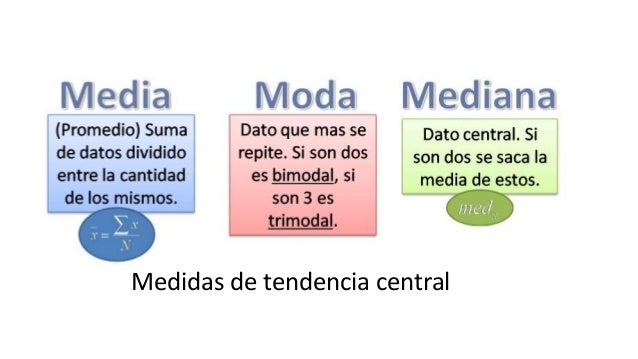
Medidas de tendencia central

Ir a la navegaciónIr a la búsqueda

Al describir grupos de diferentes observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro de la distribución de datos se denomina medida o parámetro de tendencia central o de centralización.

Cuando se hace referencia únicamente a la posición de estos parámetros dentro de la distribución, independientemente de que esté más o menos centrada, se habla de estas medidas como medidas de posición.¹​ En este caso se incluyen también los cuantiles entre estas medidas.

Entre las medidas de tendencia central tenemos:

• Media aritmética
• Media ponderada
• Media geométrica
• Media armónica
• Mediana
• Moda

Se debe tener en cuenta que existen variables cualitativas y variables cuantitativas, por lo que las medidas de posición o medidas de tendencia se usan de acuerdo al tipo de variable que se está observando, en este caso se observan variables cuantitativas.

La media aritmética es, probablemente, uno de los parámetros estadísticos más extendidos.²​ Se le llama también promedio o, simplemente, media.

Definición formal[editar]

Dado un conjunto numérico de datos, x₁, x₂, ..., x_n, se define su media aritmética como

${\displaystyle {\overline {x}}={\frac {x_{1}+x_{2}+...+x_{n}}{n}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$

Esta definición varía, aunque no sustancialmente, cuando se trata de variables continuas, esto es, también puede calcularse para variables agrupadas en intervalos

Moda[editar]

Artículo principal: Moda (estadística)

La moda es el dato más repetido de la encuesta, el valor de la variable con mayor frecuencia absoluta.Rius Díaz, Francisca. «2.3.6 La moda». Bioestadística. Métodos y aplicaciones.</ref> En cierto sentido la definición matemática corresponde con la locución "estar de moda", esto es, ser lo que más se lleva.

Su cálculo es extremadamente sencillo, pues solo necesita un recuento. En variables continuas, expresadas en intervalos, existe el denominado intervalo modal o, en su defecto, si es necesario obtener un valor concreto de la variable, se recurre a la interpolación.

Por ejemplo, el número de personas en distintos vehículos en una carretera: 5-7-4-6-9-5-6-1-5-3-7. El número que más se repite es 5, entonces la moda es 5.

Hablaremos de una distribución bimodal de los datos, cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Cuando en una distribución de datos se encuentran tres o más modas, entonces es multimodal. Por último, si todas las variables tienen la misma frecuencia diremos que no hay moda.

Cuando tratamos con datos agrupados en intervalos, antes de calcular la moda, se ha de definir el intervalo modal. El intervalo modal es el de mayor frecuencia absoluta

Mediana[editar]

Artículo principal: Mediana (estadística)

La mediana es un valor de la variable que deja por debajo de sí a la mitad de los datos, una vez que éstos están ordenados de menor a mayor.⁶​ Por ejemplo, la mediana del número de hijos de un conjunto de trece familias, cuyos respectivos hijos son: 3, 4, 2, 3, 2, 1, 1, 2, 1, 1, 2, 1 y 1, es 2, puesto que, una vez ordenados los datos: 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 4, el que ocupa la posición central es 2:

${\displaystyle {\rm {\underbrace {1,\ 1,\ 1,\ 1,\ 1,\ 1,} _{Mitad\;inferior}\;\underbrace {\color {Red}2,} _{Mediana\;}\;\underbrace {2,\ 2,\ 2,\ 3,\ 3,\ 4} _{Mitad\;superior}}}}$

En caso de un número par de datos, la mediana no correspondería a ningún valor de la variable, por lo que se conviene en tomar como mediana el valor intermedio entre los dos valores centrales. Por ejemplo, en el caso de doce datos como los siguientes:

${\displaystyle {\rm {\underbrace {1,\ 1,\ 1,\ 1,\ 1,} _{Valores\;inferiores}\;\underbrace {\color {Red}1,\ 2,} _{Valores\;intermedios}\;\underbrace {2,\ 2,\ 3,\ 3,\ 4} _{Valores\;superiores}}}}$

Se toma como mediana ${\displaystyle 1,2={\frac {{\color {Red}1}+{\color {Red}2}}{2}}}$

Existen métodos de cálculo más rápidos para datos más numerosos (véase el artículo principal dedicado a este parámetro). Del mismo modo, para valores agrupados en intervalos, se halla el "intervalo mediano" y, dentro de éste, se obtiene un valor concreto por interpolación.